Salut à tous,

Récemment je me suis penché sur un sujet que je trouve extrêmement intéressant, autant pour son côté moderne, que sa finesse ou que pour la rigueur qu’il était nécessaire d’avoir pour mener à bien toutes les étapes. Ce sujet concerne une partie des fonctions de hachage : Ceci s’appelle la technique du hash length extension.

Dans un premier temps, il faut savoir que cette technique ne marche que pour certains algorithmes de hachage, sûrement pas pour tous. Vous verrez par la suite pourquoi. Nous allons prendre dans cet article l’exemple de l’algorithme sha1 tout simplement car c’est avec lui que j’ai effectué tous mes tests.

Je vous propose alors de partir d’une vision large du sujet pour comprendre globalement le fonctionnement de cette technique avant d’entamer une explication technique agrémentée d’exemples.

Théorie

Première approche

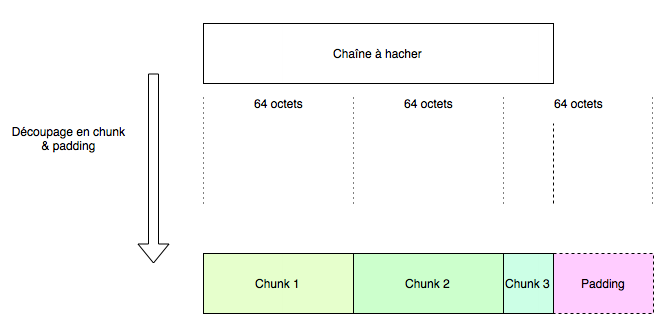
Cette technique est à la fois très simple à comprendre, relativement puissante mais assez compliquée à mettre en place sans se tromper (l’expérience parle). L’idée, c’est que l’algorithme de hachage sha1 fonctionne de la manière suivante : Lorsqu’on lui demande de hacher une chaîne de caractères, il découpe cette chaîne en blocs de taille fixe, 64 octets pour sha1. Une fois cette découpe faite, le dernier bloc doit être rempli pour faire également 64 octets. C’est l’algorithme de hachage qui s’en occupe, nous verrons les détails ensuite.

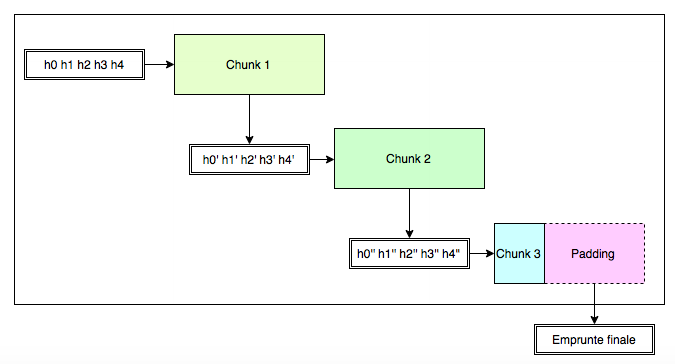
Une fois ceci fait, il hache le premier bloc, puis avec le résultat de cette empreinte, il hache le second bloc, et ainsi de suite. La dernière empreinte trouvée est alors l’empreinte de la chaîne hachée. Le bloc n est donc haché avec la seule connaissance de l’empreinte du bloc n-1.

Ainsi, il est très simple de comprendre que si nous avons haché une chaîne composée de 3 blocs, il est possible d’ajouter une information supplémentaire, sans connaitre les résultats intermédiaires. Pour cela, il suffit de prendre le résultat du hachage des 3 premiers blocs, ajouter un 4ème bloc, et calculer la nouvelle empreinte à partir de l’empreinte précédente, qui sera l’empreinte des 4 blocs.

Mais pourquoi est-ce que c’est dangereux ?

Exemple d’exploitation

Contexte

Prenons un exemple très simple. Imaginons qu’un serveur web reçoive des requêtes provenant de différents utilisateurs, et que ce serveur ait une valeur secrète MonS3cret, ainsi qu’une valeur name=hackndo&admin=0 ou name=hackndo&admin=1 si on veut qu’un utilisateur soit invité ou administrateur. Ce genre de pratique ne sera utilisée que très rarement d’une manière aussi simple à exploiter, il arrive souvent qu’elle soit un peu cachée derrière des cookies ou autres variables afin d’éviter le recours à des sessions ou une base de donnée pour vérifier l’identité de l’utilisateur une fois qu’il s’est identifié.

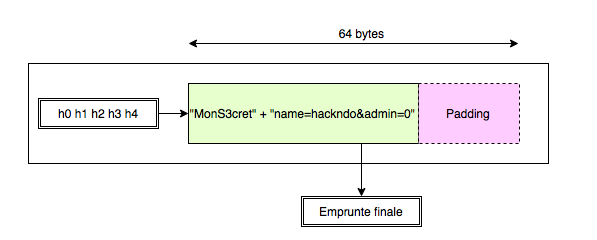
Ces valeurs étant dans l’URL, elles peuvent être facilement modifiées par l’utilisateur. Pour se protéger, le serveur ajoute une valeur dans l’url qui est sha1(MonS3cret + "name=hackndo&admin=0") ou sha1(MonS3cret + "name=hackndo&admin=1") en fonction de l’utilisateur et de ses droits. Comme la valeur MonS3cret n’est pas connue par l’utilisateur il n’est pas possible pour lui de deviner le résultat du sha1. Lorsque l’utilisateur charge une page, le serveur vérifie que les paramètres dans l’URL sont cohérents, donc que l’utilisateur n’a pas modifié la valeur de admin.

Sachant que :

sha1("MonS3cret" + "name=hackndo&admin=0") == "3e1dc496d50661d476139ee7e936d9b6822f2f62"

L’url ressemblerait à :

http://beta.hackndo.com?name=hackndo&admin=0&check=3e1dc496d50661d476139ee7e936d9b6822f2f62

L’utilisateur charge la page, le serveur reçoit tous les paramètres de l’URL précédant la variable check (name=hackndo&admin=0), effectue un sha1 avec le secret en préfixe, et vérifie l’égalité avec le paramètre check. Comme tout est correct, il charge la page.

Maintenant, l’utilisateur (qui a très envie de devenir administrateur !) change le paramètre admin=0 en admin=1. Mais comme il ne connait pas la valeur du secret, il n’est pas en mesure de trouver la valeur de check. Le serveur reçoit à nouveau les paramètres, mais cette fois-ci il détectera que le sha1 des paramètres est différent du sha1 du check qu’il avait précédemment calculé. Il refusera donc de donner les informations.

Exploitation

Souvenez-vous alors du fonctionnement de sha1. Nous avons expliqué que nous pouvions aisément ajouter des éléments à la suite d’une empreinte déjà calculée sans connaitre les étapes intermédiaires. Nous pourrions alors ajouter, par exemple &admin=1 pour obtenir la chaîne name=hackndo&admin=0&admin=1

Sachant que le dernier paramètre fait foi, nous serions administrateur, pourvu que nous soyons capable de calculer l’empreinte associée à cette nouvelle chaîne. Nous rappelons que nous ne connaissons pas la valeur secrète du serveur, il faut alors trouver une autre méthode. Pour cela, comme l’indique le schéma ci-dessous, il faut reprendre le résultat du hachage fourni par le serveur avec la valeur admin=0 et ajouter un nouveau bloc contenant la valeur &admin=1, calculer son sha1 à l’aide de l’empreinte du bloc précédent, donc celle fournie par le serveur.

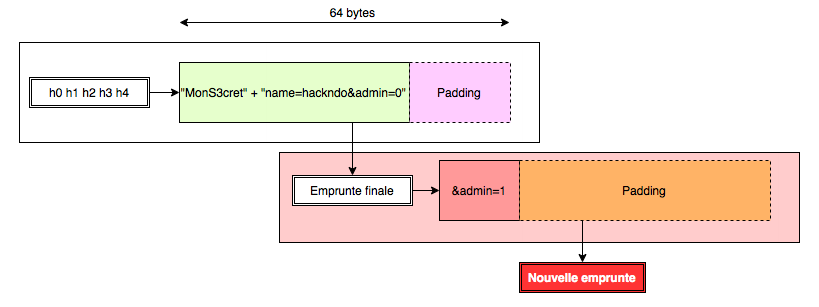La nouvelle empreinte ainsi calculée est parfaitement valide, et nous n’avons pas eu besoin d’utiliser la valeur secrète gardée par le serveur ! So far, so good.

Si vous avez suivi jusque là, c’est bien. Vous aurez remarqué cependant un petit détail : Le nouveau bloc de 64 octets est ajouté après le bloc précédent, donc après les informations originales, mais également après le padding normalement effectué par sha1. Ceci est nécessaire, et nous allons voir pourquoi avec une explication succincte du fonctionnement de sha1.

SHA1

Pour l’origine de SHA1 je vous invite à lire la page wikipedia. Nous allons ici expliquer sommairement comment cet algorithme fonctionne.

Comme expliqué en début d’article, lorsqu’une chaîne va être hachée par sha1, elle est dans un premier temps découpée en blocs de 64 octets. Le dernier bloc subit un remplissage pour avoir également une taille de 64 octets. Une fois la chaîne découpée en blocs, et que le dernier bloc fait également 64 octets, ce n’est qu’à ce moment là que les calculs sur ces différents blocs vont être effectués.

Pour chaque bloc, c’est un savant mélange entre le contenu du bloc et 5 valeurs appelées valeurs de hachage. Pour le bloc n, ces 5 valeurs de hachage sont les 5*8 octets obtenus du bloc n-1. Ceci marche très bien, mais il faut une valeur initiale pour le bloc. Ces 5 valeurs initiales sont connues et valent :

h0 = 0x67452301
h1 = 0xefcdab89
h2 = 0x98badcfe
h3 = 0x10325476
h4 = 0xc3d2e1f0

Le premier bloc est haché avec ces valeurs, ce qui fournit un sha1 intermédiaire de 40 octets. Découpés en 5 valeurs de 8 octets, ces 5 valeurs vont permettre de hacher le bloc suivant, fournissant un nouveau résultat, etc. L’empreinte qui sortira du dernier tour de hachage sera l’empreinte retenue pour l’ensemble des blocs. C’était la représentation du schéma en début d’article :

Vous devriez mieux le comprendre, à présent.

Maintenant, si nous voulons ajouter un élément à la suite du 3ème bloc sans connaitre les résultats intermédiaires, il faut partir de l’empreinte finale et calculer l’empreinte de notre nouveau bloc. Évidemment, nous ne pouvons pas mettre ce nouveau bloc pile après le Chunk 3 dans le schéma précédent. Le padding doit être conservé, car nous avons expliqué que les opérations se déroulent sur des blocs de 64 octets. Si nous modifions le dernier bloc qui a permis de calculer l’empreinte finale, alors nous modifions également cette empreinte, et nous ne pouvons plus nous en servir pour ajouter des éléments. Sachant que c’est la seule empreinte connue (nous n’avons pas accès aux résultats intermédiaires), il est primordiale de la conserver.

Comme il est primordiale de la conserver, il est primordiale de savoir calculer et reproduire le padding !

Voici ce qui se passe réellement, quand le dernier bloc est rempli pour faire 64 octets :

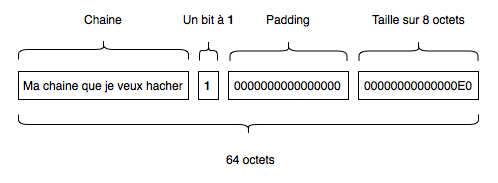
La chaîne est reçue, et la première opération effectuée est qu’un bit égal à 1 est ajouté en fin de chaîne, puis une série de zéros, et enfin la taille totale de la chaîne en bits (sans le bit ajouté, et sans les zéros), et en big endian. Cette taille est enregistrée sur 8 octets. La série de zéros est de taille variable et permet de faire en sorte que le bloc fasse bien 64 octets.

Ici la taille de notre chaîne est de 28 octets, donc 224 bits, donc 0xE0 bits.

Cas pratique

Nous avons maintenant tous les éléments en main pour passer au cas pratique ! Nous allons reprendre l’exemple de la partie théorie, mais nous allons cette fois mettre les mains dans le cambouis.

Pour rappel, nous avions une url qui ressemblait à

http://beta.hackndo.com?name=hackndo&admin=0&check=3e1dc496d50661d476139ee7e936d9b6822f2f62

Et notre but va être d’ajouter à la suite de

name=hackndo&admin=0

la valeur

&admin=1

Comme vous avez bien suivi la partie théorie, vous savez que réellement, notre chaîne ne ressemblera pas à

name=hackndo&admin=0&admin=1

Mais plutôt à quelque chose comme

name=hackndo&admin=0%80%00%00%00...%00%E8&admin=1

En effet, nous ne devons pas toucher au padding ajouté automatiquement par sha1 lorsqu’il a effectué son opération sur name=hackndo&admin=0 en nous fournissant la signature. Si nous enlevons le padding, alors l’empreinte n’est plus valide. Notre chaîne de caractères doit alors être ajoutée en fin de bloc. Mais ce n’est pas un soucis dans notre cas.

Que fait le serveur ?

Étudions ce que fait le serveur pour pouvoir le reproduire et ajouter nos informations.

Le serveur fournit à l’utilisateur une chaîne de caractères qui ne doit pas être modifiée

name=hackndo&admin=0

Et une empreinte pour vérifier qu’elle n’a pas été modifiée

sha1("MonS3cret" + "name=hackndo&admin=0")

Le serveur prend donc la chaîne que nous avons en main, la concatène avec sa valeur secrète, et produit le sha1.

Comment ce sha1 est-il calculé ? Voici à quoi il ressemble en hexadécimal

00000000  4d 6f 6e 53 33 63 72 65  74 6e 61 6d 65 3d 68 61  |MonS3cretname=ha|
00000010  63 6b 6e 64 6f 26 61 64  6d 69 6e 3d 30           |ckndo&admin=0|

Ce bloc fait moins de 64 octets. Donc, comme vu dans le paragraphe sur sha1, un bit égal à 1 va être ajouté, puis des bits à zéro, puis la taille de la chaîne en bits, en big endian. Voilà le résultat :

00000000  4d 6f 6e 53 33 63 72 65  74 6e 61 6d 65 3d 68 61  |MonS3cretname=ha|
00000010  63 6b 6e 64 6f 26 61 64  6d 69 6e 3d 30 80 00 00  |ckndo&admin=0   |
00000020  00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00  |                |
00000030  00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 E8  |                |

Voilà notre bloc de 64 octets qui va être haché par sha1 et produire l’empreinte 3e1dc496d50661d476139ee7e936d9b6822f2f62.

Nous voyons l’apparition de 3 éléments clés : Le premier est la valeur 0x80 qui suit directement le message original. Il se trouve que 0x80 a pour représentation binaire 10000000. C’est donc bien un 1 puis des 0x00 qui ont été ajoutés à la suite du message.

Le deuxième est alors la suite de 0x00 qui permet de faire en sorte que le bloc fasse 64 octets.

Enfin, les 8 derniers octets

00 00 00 00 00 00 00 E8

sont utilisés pour la taille du message original en bits, en big endian (29 octets, 232 bits, donc 0xE8 bits).

Comment le reproduire ?

Trouver le padding

La première étape va être de calculer le padding qui a été ajouté automatiquement, afin de pouvoir reproduire le bloc de 64 octets ayant fourni la signature 3e1dc496d50661d476139ee7e936d9b6822f2f62.

Théoriquement, nous n’avons pas connaissance de la valeur secrète, donc nous ne connaissons pas sa taille. Nous ne connaissons donc pas le nombre de zéros à mettre pour le padding, ni la taille à indiquer en fin de bloc. Il faut donc, en pratique, essayer avec différentes longueurs jusqu’à trouver celle qui correspond. Pour gagner du temps, nous allons directement prendre la longueur qui correspond, c’est à dire 9 octets.

Ajouter notre message

Maintenant que nous avons le padding, nous pouvons ajouter notre message à la suite. Comme le premier bloc fait 64 octets, notre message ajouté commencera juste au début du deuxième bloc, comme cela :

00000000  ?? ?? ?? ?? ?? ?? ?? ??  ?? 6e 61 6d 65 3d 68 61  |?????????name=ha|
00000010  63 6b 6e 64 6f 26 61 64  6d 69 6e 3d 30 80 00 00  |ckndo&admin=0   |
00000020  00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 00  |                |
00000030  00 00 00 00 00 00 00 00  00 00 00 00 00 00 00 E8  |                |
00000040  26 61 64 6d 69 6e 3d 31                           |&admin=1        |

Nous avons alors le message complet que nous allons envoyer au serveur :

"name=hackndo&admin=0" + "\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xE8" + "&admin=1"

Calcul de la signature

La dernière chose à faire est de calculer la signature de ce nouveau message. Je rappelle qu’avant d’être signé, la valeur secrète va être ajoutée en début de message. Une fois ceci fait, il va être découpé en deux blocs. Le premier bloc que nous avons pris soin de créer est exactement le même que celui produit par sha1 lorsque nous ne lui passions que la chaîne originale avec admin=0. Nous sommes en possession de cette sortie de hachage, qui est 3e1dc496d50661d476139ee7e936d9b6822f2f62`.

Il suffit alors de prendre le deuxième bloc et de le hacher avec cela. Nous découpons l’empreinte du premier bloc en 5 valeurs

h1' = 0x3e1dc496
h2' = 0xd50661d4
h3' = 0x76139ee7
h4' = 0xe936d9b6
h5' = 0x822f2f62

Avec ces valeurs et notre bloc, le calcul du nouveau sha1 se fait très bien. Il est nécessaire pour cela d’avoir une implémentation de l’algorithme sha1 pour un bloc. En voici un exemple en python :

import struct, sys, hashlib

def rotate_left(num, bits):
    left = num << bits
    right = num >> (32 - bits)
    return left + right

def padding(msg, size):
    size *= 8
    padding = 64*8 - ((size + 8) % 512) - 64 # +8 octets pour le \x80 et -64 parce que la taille est sur 64 bits (8 octets)

    msg += "\x80"

    ret = msg + (padding / 8) * "\x00" + struct.pack(">q", size) # Big endian
    return ret;

def sha1_custom(chunk, h0, h1, h2, h3, h4):
    chunk = padding(chunk, 64 + len(chunk))
    words = {}
    for i in range(0, 16):
        word = chunk[i*4 : (i+1)*4]
        (words[i],) = struct.unpack(">i", word)
    
    for i in range(16, 80):
        words[i] = rotate_left((words[i-3] ^ words[i-8] ^ words[i-14] ^ words[i-16]) & 0xffffffff, 1)

    a = h0
    b = h1
    c = h2
    d = h3
    e = h4

    for i in range(0, 80):
        if 0 <= i <= 19:
            f = d ^ (b & (c ^ d))
            k = 0x5a827999
        elif 20 <= i <= 39:
            f = b ^ c ^ d
            k = 0x6ed9eba1
        elif 40 <= i <= 59:
            f = (b & c) | (b & d) | (c & d)
            k = 0x8f1bbcdc
        elif 60 <= i <= 79:
            f = b ^ c ^ d
            k = 0xca62c1d6

        a, b, c, d, e = (rotate_left(a, 5) + f + e + k + words[i]) & 0xffffffff, a, rotate_left(b, 30), c, d

    h0 = (h0 + a) & 0xffffffff
    h1 = (h1 + b) & 0xffffffff
    h2 = (h2 + c) & 0xffffffff
    h3 = (h3 + d) & 0xffffffff
    h4 = (h4 + e) & 0xffffffff
    return '%08x%08x%08x%08x%08x' % (h0, h1, h2, h3, h4)

La fonction sha1_custom permet de calculer une itération sur un bloc avec des valeurs h0, h1, h2, h3 et h4 variables.

En lançant cette fonction avec nos informations, nous obtenons le résultat suivant :

print sha1_custom("&admin=1", int(0x3e1dc496), int(0xd50661d4), int(0x76139ee7), int(0xe936d9b6), int(0x822f2f62))
# Output : 18fd6206c61138eee7f99a73bf9172f9b28acb61

Voici notre emprunte calculée ! Nous pouvons vérifier qu’elle est bien égal à celle fournie par le serveur si nous lui envoyons notre message forgé :

print hashlib.sha1("MonS3cret" + "name=hackndo&admin=0" + "\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xe8" + "&admin=1").hexdigest()
# Output : 18fd6206c61138eee7f99a73bf9172f9b28acb61

Voilà ! Nous avons prédit correctement la valeur de l’empreinte sans même connaitre la valeur secrète ! (Mais avec un petit raccourci, nous connaissions sa longueur. Mais faire une dizaine de tentatives, ce n’est pas non plus très long une fois qu’on a bien compris !)

Pour conclure, nous enverrons à notre serveur web les paramètres suivants :

name=hackndo&admin=0%80%00%00%00...%00%A0&admin=1&check=18fd6206c61138eee7f99a73bf9172f9b28acb61

Le serveur va alors prendre tous les éléments qui précèdent le check, puis préfixer cela avec la valeur secrète, calculer le sha1, et vérifier cette valeur avec notre valeur dans la variable `check. Comme c’est bien la même, nous voilà administrateur !

J’espère que cet article vous a plu. Du fait de sa complexité, si jamais des éléments ne sont pas clairs, surtout n’hésitez pas à poster des commentaires, je m’efforcerai d’y répondre au mieux, as usual.

Hash length extension