Nous allons dans cet article parler de la technique d’attaque du padding oracle, en utilisant le padding d’un message chiffré suite à un chiffrement par bloc utilisant le mode CBC.

Il existe deux grandes familles de chiffrement. Les chiffrements symétriques pour lesquels une même clé est utilisée pour le chiffrement et le déchiffrement, et les chiffrements asymétriques qui possèdent une clé pour le chiffrement et une autre pour le déchiffrement.

En ce qui concerne les chiffrement symétrique, les données peuvent être chiffrées de deux manières. Il existe les chiffrements de flux, c’est à dire qu’une longueur quelconque de donnée peut être chiffrée, les données n’ont pas besoins d’être découpées. L’autre manière est le chiffrement par blocs. Dans ce cas là, les données sont découpées en blocs de taille fixe afin de pouvoir être chiffrées.

Enfin, différents modes d’opérations sont possibles pour le chiffrement par bloc, tels que CBC, ECB, CFB etc.

Cependant, le chiffrement par bloc lève deux questions

• Que se passe-t-il si la taille du message à chiffrer n’est pas un multiple de la taille d’un bloc ? Donc que se passe-t-il si le dernier bloc a une taille inférieure aux autres blocs ?
• Que se passe-t-il si une fois le texte clair découpé, deux blocs clairs sont identiques ? Leur chiffrement ne doit pas donner deux résultats similaires car d’un point de vue cryptographique, un attaquant pourra deviner que des morceaux du texte clair sont identiques, ce qui n’est pas souhaitable.

Nous allons dans cet article nous intéresser au mode CBC du chiffrement par blocs qui permet de répondre à la deuxième question.

Fonctionnement du mode CBC

Padding

Alors que nous avons parlé du padding utilisé par les fonctions de hashage dans l’article sur le Hash Length Extension, nous allons ici nous intéresser à une technique de padding majoritairement utilisée dans les chiffrements par blocs, PKCS7 dont le fonctionnement est décrit dans la RFC 5652.

Soit N octets la taille d’un bloc. S’il manque M octets dans le dernier bloc, alors on ajoutera le charactère ‘0xM’ M fois à la fin du bloc.

Par exemple, si nous avons des blocs de taille 8 octets et que nous avons le texte clair suivant :

"Love hackndo"

Le découpage donnera

"Love hac"
"kndo"

Il manque alors 4 octets pour que le dernier bloc “kndo” fasse 8 octets. Le padding sera alors le suivant

"kndo\x04\x04\x04\x04"-

Dans le cas où la taille du texte est un multiple de la taille d’un bloc, alors un bloc entier de padding est ajouté à la suite du texte clair. En effet, imaginons deux données en clair :

# Données 1
"\x41\x42\x41\x42\x41\x42\x41\x42"
"\x43\x44\x43\x44\x43\x44\x43\x01"

# Données 2
"\x41\x42\x41\x42\x41\x42\x41\x42"
"\x43\x44\x43\x44\x43\x44\x43"

Dans les premières données en clair, le \x01 fait partie de l’information à transmettre. Si jamais aucun padding n’était ajouté, alors on ne pourrait pas différencier les données 1 des données 2 suite au padding. L’ajout d’un bloc complet permet ainsi de différencier ces cas.

Après padding, nous avons alors

# Données 1 après padding
"\x41\x42\x41\x42\x41\x42\x41\x42"
"\x43\x44\x43\x44\x43\x44\x43\x01"
"\x08\x08\x08\x08\x08\x08\x08\x08"

# Données 2 après padding
"\x41\x42\x41\x42\x41\x42\x41\x42"
"\x43\x44\x43\x44\x43\x44\x43\x01"

Les deux données claires après padding sont différentes, ce qui donnera des chiffrements différents, chose que l’on souhaite puisque les données initiales sont différentes.

Voici un petit code python qui propose deux fonctions. L’une ajoute le padding nécessaire au dernier bloc, et l’autre supprime le padding.

def set_padding(data, size_block=128):
    if size_block % 8 != 0:
        return False
    size_block_byte = size_block/8
    padding = size_block_byte - (len(data) % size_block_byte)
    data += chr(padding)*padding

    return data

def del_padding(data):
    return data[:-ord(data[-1])]

# Exemple

data = "Love hackndo!"
data_padded = set_padding(data, 64)
print([data_padded])
# >>> ['Love hackndo!\x03\x03\x03']

data_padding_removed = del_padding(data_padded)
print([data_padding_removed])
# >>> ['Love hackndo!']

data = "12345678"
data_padded = set_padding(data, 64)
print([data_padded])
# >>> ['12345678\x08\x08\x08\x08\x08\x08\x08\x08']

data_padding_removed = del_padding(data_padded)
print([data_padding_removed])
# >>> ['12345678']

Nous parlons de padding oracle non pas en lien avec Oracle l’entreprise, mais car l’oracle est la partie (souvent) serveur qui donne l’information sur la validité - ou non - du padding d’un message chiffré, permettant l’attaque dont nous allons parler par la suite.

Blocs similaires

Le mode CBC permet de pallier au problème des blocs similaires. Imaginons que nous avons des blocs de 32 bits, et que le message que nous voulons coder est le suivant “hack, or do not hack”. En découpant ce message en blocs de 32 bits (donc 4 octets), nous obtenons ces 5 blocs

"hack"
", or"
" do "
"not "
"hack"

Si chaque bloc est chiffré indépendamment, alors le premier et le dernier bloc de notre message donneront le même texte chiffré, ce qui n’est pas souhaitable comme précédemment indiqué.

Dans le mode CBC, pour obtenir le chiffrement d’un bloc de texte clair, ce texte clair est XORé avec le texte chiffré du bloc précédant, avant d’être lui même chiffré.

On a alors

bloc_n_chiffré = chiffrement(bloc_n_clair ⊕ bloc_n-1_chiffré)

Si vous avez bien compris ce principe, vous devriez vous demander ce qu’il se passe pour chiffrer le premier bloc, puisqu’il n’y a pas de bloc avant lui pour effectuer ce XOR.

Et bien pour cela, un IV (Initialization Vector) est défini, c’est à dire une chaine aléatoire choisie pour ce chiffrement d’une taille égale à la taille d’un bloc. Cet IV permet de simuler un bloc précédant. Vous obtenez alors le schéma suivant :

En termes mathématiques, voici comment un chiffrement CBC fonctionne

# Pour n = 0:

bloc_n_chiffré = chiffrement(bloc_n_clair ⊕ IV)

# Pour n > 0:

bloc_n_chiffré = chiffrement(bloc_n_clair ⊕ bloc_n-1_chiffré)

Du coup, grâce au propriétés de l’opération XOR, voici à quoi ressemble en terme mathématiques le déchiffrement

# Pour n = 0:

bloc_n_clair = déchiffrement(bloc_n_chiffré) ⊕ IV

# Pour n > 0:

bloc_n_clair = déchiffrement(bloc_n_chiffré) ⊕ bloc_n-1_chiffré

Vulnérabilité du mode CBC

Du chiffrement au XOR

Maintenant que nous avons les mathématiques avec nous, nous pouvons créer et combiner quelques informations. Accrochez-vous, suivez bien, il n’y a rien de magique.

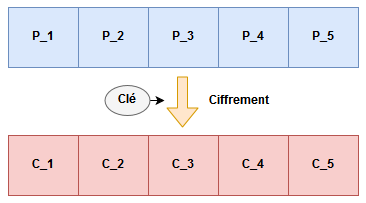
Prenons un exemple théorique, une chaine de caractères qui, une fois paddée, fait 5 blocs de 8 octets chacun. Les 5 blocs de plaintext sont P_1 .. P_5 et les 5 blocs chiffrés sont C_1 .. C_5.

Nous avons donc le schéma suivant :

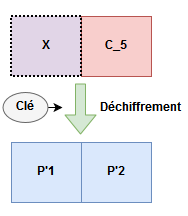
Maintenant, prenons un nouveau bloc X totalement aléatoire. C’est un bloc que nous créons, que nous maitrisons, qu’on peut changer, frapper, manger. Prenons avec lui le dernier bloc chiffré de notre exemple, C_5, et concaténons les.

Nous avons alors le schéma suivant :

Nous pouvons, à l’aide de ce que nous avons vu avant, écrire P'2 de la manière suivante

# Égalité 1
P'2 = déchiffrement(C_5) ⊕ X

Nous avons également la formule suivante pour C_5

# Égalité 2
C_5 = chiffrement(P_5 ⊕ C_4)

Donc en remplaçant C_5 dans l’égalité 1 par sa représentation dans l’égalité 2 on obtient

P'2 = déchiffrement(chiffrement(P_5 ⊕ C_4)) ⊕ X

# Or déchiffrer un texte chiffré donne le texte original, donc

P'2 = P_5 ⊕ C_4 ⊕ X

Nous voilà avec une équation qui relie 2 éléments connus avec deux inconnues

Connus

• X : C’est l’élément que nous maitrisons, que nous pouvons changer, frapper, manger
• C_4 : C’est l’avant dernier bloc du chiffrement.

Inconnus

• P_5 : Le dernier bloc de plaintext de la chaine, ce que nous cherchons à trouver
• P'2 : Le bloc de plaintext associé à la concaténation de X et de C_5

Cette équation ne possède plus de cryptographie, seulement du XOR. Nous avons fait sauter l’aspect cryptographique seulement avec des mathématiques.

Pour pouvoir résoudre cette équation qui pour le moment possède deux inconnues, nous faisons entrer en jeu nos connaissances sur le padding oracle.

Invoquons l’oracle

Nous avons donc l’égalité suivante grâce à notre raisonnement mathématique

P'2 = P_5 ⊕ C_4 ⊕ X

# Donc

P_5 = P'2 ⊕ C_4 ⊕ X

Cette égalité ne contient que l’opération XOR. Comme vous le savez, le XOR est une opération bit à bit, nous pouvons donc découper cette égalité en la calculant octet par octet. Nos blocs faisant 8 octets, nous avons les équations suivantes :

P_5[0] = P'2[0] ⊕ C_4[0] ⊕ X[0]
P_5[1] = P'2[1] ⊕ C_4[1] ⊕ X[1]
P_5[2] = P'2[2] ⊕ C_4[2] ⊕ X[2]
P_5[3] = P'2[3] ⊕ C_4[3] ⊕ X[3]
P_5[4] = P'2[4] ⊕ C_4[4] ⊕ X[4]
P_5[5] = P'2[5] ⊕ C_4[5] ⊕ X[5]
P_5[6] = P'2[6] ⊕ C_4[6] ⊕ X[6]
P_5[7] = P'2[7] ⊕ C_4[7] ⊕ X[7]

Nous savons par ailleurs que le déchiffrement d’un texte chiffré doit donner un plaintext avec un padding valide, donc se terminant par 0x01 ou 0x02 0x02 etc. Comme nous contrôlons tous les octets de X, nous pouvons bruteforcer le dernier octet jusqu’à ce que l’algorithme de déchiffrement renvoie du texte valide. Dans ce cas-là, ça voudra dire que le padding du texte clair est valide, donc qu’il termine par 0x01.

Nous ne prenons pas en compte les faux-positifs dans cet article. En effet, il y a une (faible) chance que le clair se termine par 0x02 0x02 ou d’autres padding, mais ces cas sont rares. Je ferai peut-être une mise à jour de l’article pour les prendre en compte plus tard.

Une fois qu’on a trouvé l’octet qui donne le padding valide, donc le padding 0x01, en ne prenant l’égalité que sur le dernier octet (donc d’indice 7, puisque nos blocs font 8 octets) …

P_5[7] = P'2[7] ⊕ C_4[7] ⊕ X[7]

… nous pouvons résoudre l’égalité puisque nous connaissons P'2[7] qui est justement 0x01, mais également X[7] qui est la valeur du bruteforce et C_4[7] qui est dans le texte chiffré reçu.

Avec toutes ces informations, nous trouvons donc le dernier octet du dernier bloc de plaintext du texte (qui est du padding, mais c’est un bon début) !

Maintenant, pour retrouver l’octet précédent (donc d’indexe 6), il suffit choisir X[7] tel que P'2[7] = 0x2 puis de bruteforcer X[6] pour que le padding soit valide. Quand nous avons une valeur pour X[6] qui donne un padding valide, cela signifie qu’on a également P'2[6] = 0x2, et donc on peut résoudre l’égalité

P_5[6] = P'2[6] ⊕ C_4[6] ⊕ X[6]

car nous avons toutes les valeurs en main.

Ce raisonnement est à faire en boucle jusqu’à trouver toutes les valeurs du plaintext du bloc.

Une fois le bloc déchiffré, il suffit de prendre les autres blocs et d’appliquer exactement le même raisonnement. On trouve comme ça les blocs P_4, P_3 et P_2.

Un problème se pose cependant pour trouver le bloc P_1. En effet, pour les cas précédents, nous nous basions sur la connaissance du bloc chiffré qui précédait le bloc en cours de déchiffrement. Cependant, pour le premier bloc, il faut connaitre l’IV utilisé. Dans ce cas, pas de miracle :

• Soit vous connaissez l’IV, auquel cas c’est le même raisonnement,
• Soit vous essayez de le deviner en utilisant des combinaisons usuelles, telles qu’un IV nul, ou une suite d’octets consécutifs.

Si jamais vous ne pouvez pas le trouver, alors il faudra vous contenter du déchiffrement des blocs 2 à N.

Script python

Je vous mets à disposition le script python que j’ai écrit pour du chiffrement AES128 CBC

#/usr/bin/env python3

from Crypto.Cipher import AES
BLOCK_SIZE = 128
key = '0123456789abcdef'
IV = BLOCK_SIZE // 8 * '\x00'
mode = AES.MODE_CBC

"""
Chiffrement AES 128 CBC
"""
def encipher(plain):
    encryptor = AES.new(key, mode, IV=IV)
    padded_plain = set_padding(plain)
    return encryptor.encrypt(padded_plain)


"""
Déchiffrement AES 128 CBC
Renvoi False si le padding n'est pas valide
"""
def decipher(cipher):
    decryptor = AES.new(key, mode, IV=IV)
    plain_padded = decryptor.decrypt(cipher)
    if not is_padding_valid(plain_padded):
        return False
    return plain_padded

"""
Ajoute le padding en fonction de la taille d'un bloc
"""
def set_padding(data, size_block=BLOCK_SIZE):
    if size_block % 8 != 0:
        return False
    size_block_byte = size_block//8
    padding = size_block_byte - (len(data) % size_block_byte)
    data += chr(padding)*padding
    return data


"""
Supprime le padding
"""
def del_padding(data):
    return data[:-data[-1]]


"""
Vérifie la validité du padding
"""
def is_padding_valid(data):
    if len(data) == 0:
        return False
    c = data[-1]
    return data[-c:] == bytes([c])*c

"""
Découpe un buffer en blocs en fonction de la taille fournie
"""
def get_blocks(data, size_block=BLOCK_SIZE):
    return [data[i*(size_block//8):(i+1)*(size_block//8)] for i in range(len(data)//(size_block//8))]

"""
Déchiffrement du message
Si l'IV est fourni, alors le premier bloc est également déchiffré
"""
def decrypt(cipher, IV=None, block_size=BLOCK_SIZE):
    cipher_blocks = get_blocks(cipher)
    res = b""
    if IV is not None:
        cipher_blocks = [bytes(IV, "utf-8")] + cipher_blocks

    # Les blocs sont déchiffrés un à un
    for _ in range(len(cipher_blocks)-1):
        plain = b""
        last_cipher_block = cipher_blocks[-1]
        trail = b""

        # Pour chaque bloc, on déchiffre octet par octet
        for k in range(block_size//8):

            # Bruteforce pour trouver l'octet qui donne le bon padding
            for i in range(256):
                flip = bytes([i])
                cipher_block_attack = (15-k) * b'\x00' + flip + trail
                cipher_both_block =b"".join([cipher_block_attack, last_cipher_block])

                # On vérifie la validité du padding suite à un déchiffrement
                if decipher(cipher_both_block):
                    last_plain = (k+1) ^ cipher_blocks[-2][15-k] ^ i
                    plain = bytearray([last_plain]) + plain
                    trail = b""

                    # Si le bon padding est trouvé, le bloc contrôlé (X dans l'article) est mis à jour
                    for l in range(k+1):
                        last_byte = (k+2) ^ plain[-l-1] ^ cipher_blocks[-2][15-l]
                        trail = bytearray([last_byte]) + trail
                    break

        # Suppression du bloc déchiffré
        cipher_blocks = cipher_blocks[:-1]
        res = plain + res
        
    return del_padding(res)


plain = "This is the s3cret key boyz so let's go to work :D"
ciphered = encipher(plain)

print(decrypt(ciphered, IV))

Lorsqu’on exécute le programme, on obtient bien le résultat escompté

$ python padding_oracle.py 
bytearray(b"This is the s3cret key boyz so let\'s go to work :D")

Pisse love flex !